Física 1er Parcial Sep 19 TF6 – D3 Dinámica

D3. En el sistema de la figura, los carritos A y B (de masas mA = 5 kg y mB = 3 kg) se encuentran inicialmente en reposo, vinculados por una soga ideal. A t = 0 s se aplica una fuerza F horizontal constante sobre A. Se desprecian todos los rozamientos. En esas condiciones, el sistema asciende con una aceleración de módulo 2,5 m/s².

a. Realice un diagrama de cuerpo libre para cada carrito, y calcule la intensidad de la fuerza F.

DCL

Ecuaciones de Newton según el eje x

Carrito A -------- Fx – T – PAx = mA a

Carrito B ------------- T – PBx = mB a

donde

PAx = componente según x del Peso A = mA g sen 37º

PBx = componente según x del Peso B = mB g sen 37º

Fx = componente según x de F = F cos 37º

T = tensión

mA = masa A = 5 kg

mB = masa B = 3 kg

a = aceleración del sistema = 2,5 m/s²

Sumando ambas ecuaciones

Fx – PAx – PBx = mA a +mB a

Reemplazando y despejando Fx

F cos 37º = mA g sen 37º + mB g sen 37º + mA a +mB a = (mA + mB) (g sen 37º + a )

F = (5 kg + 3 kg) (10 m/s² sen 37º + 2,5 m/s² ) / cos 37º  = 85 N

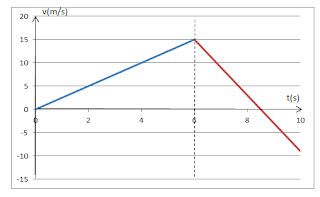
b. A los 6 segundos de comenzando el movimiento se corta la soga. Grafiqué la velocidad del carrito B en función del tiempo para los instantes t ε [0s ; 10s]. Indique los valores característicos que permiten describir dicho movimiento

Tramo I ( 0< t < 6s)

Ecuación horaria de la velocidad

vB (t) = voB + a t

donde

vB = velocidad

voB = velocidad inicial = 0 (parte del reposo)

a = aceleración del sistema = 2,5 m/s²

t = tiempo transcurrido

reemplazando

vB(t) = 2,5 m/s²  t 

vB(6s) = 2,5 m/s² 6 seg = 15 m/s  --------- velocidad final del Tramo I

Tramo II (6 s < t )

Newton ------------- – PBx = mB a2

donde

PBx = componente según x del Peso B = mB g sen 37º

a2 = aceleración  del tramo II

reemplazando y despejando a2

a2 = - mB g sen 37º / mB = - 10 m/s²  sen 37º = - 6 m/s² 

Ecuación horaria de la velocidad

vB (t) = vo2B + a2 (t – to)

donde

vB = velocidad

vo2B = velocidad inicial del tramo II = velocidad final del tramo I = 15 m/s

to = tiempo inicial del tramo II = 6 seg

reemplazando

vB(t) = 15 m/s – 6 m/s²  (t – 6s)

gráfico