Física 2do Parcial Nov19 T621 2 – D1 Dinámica

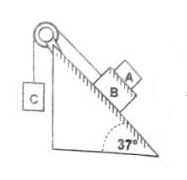
D1. En el sistema de la figura hay rozamiento entre los bloques A (mA = 1 kg) y B (mB = 2 kg) y entre el plano inclinado y B. Los coeficientes de rozamiento entre todas las superficies son μe = 0,9 y μd = 0,4. El bloque B está unido a un tercer bloque C (mc = 3 kg) por medio de una soga ideal que pasa por una polea fija, también ideal.

D1.a. Sabiendo que el bloque A no desliza respecto de B, calcule la intensidad de la fuerza de rozamiento que actúa sobre A. Indique claramente su sentido.

DCL

Cuerpo A

Según x ----- > ∑F = FrozBA – PAx = mA a

Según y ----- > ∑F = FBA – PAy = 0

Cuerpo B

Según x ----- > ∑F = T - FrozAB - FrozBP - PBx = mB a

Según y ----- > ∑F = FPB  – FAB – PBy = 0

Cuerpo C

Según x ----- > ∑F = PC – T = mC a

donde

FrozBA = fuerza de rozamiento ejercida por B sobre A

FrozAB = fuerza de rozamiento ejercida por A sobre B

| FrozAB | = | FrozBA | Par de acción-reacción

FrozBP = fuerza de rozamiento ejercida por el plano sobre B = μd FPB

μd = coeficiente de rozamiento dinámico = 0,4

FPB = fuerza ejercida por el plano sobre B

FBA = fuerza ejercida por B sobre A

FAB = fuerza ejercida por A sobre B

| FAB | = | FBA | Par de acción-reacción

PAx = componente según x del peso de A = PA sen 37º = 0,60 PA

PAy = componente según y del peso de A = PA cos 37º = 0,80 PA

PA = peso de A = mA g = 1 kg 10 m/s² = 10 N

mA = masa de A = 1 kg

PBx = componente según x del peso de B = PB sen 37º = 0,60 PB

PBy = componente según y del peso de B = PB cos 37º = 0,80 PB

PB = peso de B = mB g = 2 kg 10 m/s² = 20 N

mB = masa de B = 2 kg

PC = peso de C = mC g = 3 kg 10 m/s² = 30 N

mC = masa de C = 3 kg

T = tensión de la soga B y C

a = aceleración del sistema (los tres cuerpos se mueven juntos)

Calculando FrozBP

FrozBP = μd FPB = μd (FAB + PBy) = μd (PAy + PBy) = 0,4 (0,8 * 10 N + 0,8 * 20 N) = 9,6 N

Sumando las tres ecuaciones según x

PC - PAx - FrozBP – PBx = mA a + mB a + mC a

Reemplazando y despejando a

a = (PC - PAx - FrozBP – PBx) / (mA + mB + mC)

a = (30 N - 0,6 * 10 N - 9,6 N - 0,6 * 20 N) / (1 kg + 2 kg + 3 kg) = 0,4 m/s²

Reemplazando en la ecuación según x del cuerpo A y despejando FrozBA

FrozBA =  mA a + PAx = 1 kg * 0,4 m/s²  + 0,60 * 10 N = 6,4 N en sentido x positivo (sube)

D1.b. Cuál es el valor máximo que puede tener la masa del bloque C para que A no deslice sobre B?

Fuerza de rozamiento estático máximo entre A y B

μe = coeficiente de rozamiento estático = 0,9

Froz max = μe FAB = μe PAy = 0,9 * 0,8 * 10 N = 7,2 N

Reemplazando en la ecuación según x del cuerpo A y despejando a

a = (FrozBA – PAx) / mA  = (7,2 N – 0,6 * 10 N) / 1 kg = 1,2 m/s²

Sumando las tres ecuaciones según x

mC g - PAx - FrozBP – PBx = mA a + mB a + mC a

Reemplazando y despejando mC

mC = (PAx + FrozBP + PBx + mA a + mB a) / (g – a)

mC = (0,6 * 10 N + 9,6 N + 0,6 * 20 N + 1 kg 1,2 m/s² + 2 kg 1,2 m/s²) / (10 m/s² – 1,2 m/s²)

mC = 3,54 kg ------ masa máxima de C