Dinámica – 47 Fuerza de rozamiento

Dinámica 47. (Opcional) Un mujer de masa m_M está parada sobre un bloque de masa m_B = 3 m_M. Entre ellos el coeficiente de rozamiento es μ. El bloque está sobre un piso horizontal sin rozamiento. La mujer está tomada de una soga ideal y las poleas también son ideales.

a) Realizar el diagrama de cuerpo libre para la mujer, el bloque y las poleas e indicar las fuerzas exteriores e interiores para el sistema formado solo por la mujer y el bloque.

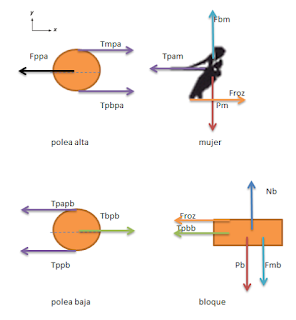
DCL

Polea alta

Fppa = Fuerza ejercida por la pared sobre la polea alta

Tmpa = Tensión ejercida por la mujer sobre la polea alta

Tpbpa = Tensión ejercida por la polea baja sobre la polea alta

Mujer

Pm = peso de la mujer

Tpam = Tensión ejercida por la polea alta sobre la mujer

Fbm  = Fuerza ejercida por el bloque sobre la mujer

Froz = Fuerza de rozamiento entre el bloque y la mujer

Polea baja

Tpapb = Tensión ejercida por la polea alta sobre la polea baja

Tbpb = Tensión ejercida por el bloque sobre la polea baja

Tppb = Tensión ejercida por la pared sobre la polea baja

Bloque

Froz = Fuerza de rozamiento entre la mujer y el bloque

Nb = Fuerza que ejerce el piso sobre el bloque

Pb = Peso del bloque

Fmb = Fuerza ejercida por la mujer sobre el bloque

Tpbb = Tensión ejercida por la polea baja sobre el bloque

Sistema mujer - bloque

Fuerzas internas

Mujer

Fbm  = Fuerza ejercida por el bloque sobre la mujer

Froz = Fuerza de rozamiento entre el bloque y la mujer

Bloque

Froz = Fuerza de rozamiento entre la mujer y el bloque

Fmb = Fuerza ejercida por la mujer sobre el bloque

Fuerzas externas

Mujer

Pm = peso de la mujer

Tpam = Tensión ejercida por la polea alta sobre la mujer

Bloque

Nb = Fuerza que ejerce el piso sobre el bloque

Pb = Peso del bloque

Tpbb = Tensión ejercida por la polea baja sobre el bloque

b) Calcular, justificando cada paso, la aceleración máxima del bloque para que la mujer no deslice sobre él.

| Tmpa | = | Tpam | par acción- reacción

| Tpbpa | = | Tpapb | par acción – reacción

| Tmpa | = | Tpbpa | polea fija

| Tmpa | = | Tpam | = | Tpbpa | = | Tpapb | = Tm

| Tbpb | = | Tpbb | par acción reacción = Tb

| Fbm | = | Fmb | par acción reacción

Ecuaciones de Newton

Polea alta según x ----- > ∑F = - Tppa + Tm + Tm = 0

Mujer según x ----- > ∑F = - Tm + Froz = mm (-a)

Mujer según y ----- > ∑F = - Pm + Fbm = 0

Polea baja según x ----- > ∑F = - Tm – Tm + Tb = 0

Bloque según x ----- > ∑F = - Tb - Froz = mb (-a)

Bloque según y ----- > ∑F = Nb - Pm - Fbm = 0

despejando Fbm de la ecuación según x de la mujer

Fbm = Pm = mm g

calculando Froz

Froz = μ Fbm = μ mm g

despejando Tm y Tb de las ecuaciones según x de la mujer y el bloque

Tm = mm a + Froz

Tb  = mb a - Froz

reemplazando Froz y Tb y Tm en la ecuación de la polea baja

Tb = 2 Tm

mb a - μ mm g = 2 (mm a + μ mm g)

reemplazando mb = 3mm

3 mm a - μ mm g = 2 mm a + 2 μ mm g

despejando a

a = 3 μ g  < ----------- aceleración máxima