Dinámica – 46 Fuerza de rozamiento

Dinámica 46. Dos bloques, que pesan 8 kgf y 80 kgf respectivamente, están unidos por una barra de masa despreciable y deslizan hacia abajo sobre un plano inclinado 30º respecto de la horizontal. El coeficiente de rozamiento dinámico entre el bloque de menos masa y el plano es 0,25 y el correspondiente al otro bloque es 0,5.

a) i) Calcular la aceleración y la tensión en la barra.

Para determinar la ubicación relativa de los bloques (cual va arriba y cual va abajo), analizamos los bloques independientemente (sin la barra). El que tenga mayor aceleración, “arrastrara” al otro.

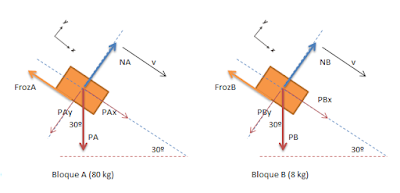
DCL (sin barra)

Ecuaciones de Newton

Bloque A según x ----- > ∑F = - FrozA + PAx = mA aA

Bloque A según y ----- > ∑F = NA – PAy = 0

Bloque B según x ----- > ∑F = - FrozB + PBx = mB aB

Bloque B según y ----- > ∑F = NB – PBy = 0

donde

FrozA = fuerza de rozamiento dinámica entre el bloque A y el plano = μdA NA

μdA = coeficiente de rozamiento dinámico entre el bloque A y el plano = 0,5

NA = fuerza que ejerce el plano sobre el bloque A

PA = Peso del boque A =  mA g

PAx = PA sen 30º

PAy = PA cos 30º

mA = masa del bloque A = 80 kg

aA = aceleración del bloque A

FrozB = fuerza de rozamiento dinámica entre el bloque B y el plano = μdB NB

μdB = coeficiente de rozamiento dinámico entre el bloque B y el plano = 0,25

NB = fuerza que ejerce el plano sobre el bloque B

PB = Peso del boque B =  mB g

PBx = PB sen 30º

PBy = PB cos 30º

mB = masa del bloque B = 8 kg

aB = aceleración del bloque B

despejando NA y NB  de las ecuaciones según y

NA = PAy = mA g cos 30º 

NB = PBy = mB g cos 30º 

calculando FrozA y FrozB

FrozA = μdA NA = μdA mA g cos 30º

FrozB = μdB NB = μdB mB g cos 30º

reemplazando las FrozA y FrozB en las ecuaciones según x, y despejando aA y aB

aA = g ( sen 30º - μdA cos 30º ) = 10 m/s² ( sen 30º - 0,5 cos 30º ) = 0,67 m/s²

aB = g ( sen 30º - μdB cos 30º ) = 10 m/s² ( sen 30º - 0,25 cos 30º ) = 2,83 m/s²

El bloque B “arrastra” al bloque A.

DCL (con barra)

Ecuaciones de Newton

Bloque A según x ----- > ∑F = - FrozA + PAx + Fbarra = mA aA

Bloque A según y ----- > ∑F = NA – PAy = 0

Bloque B según x ----- > ∑F = - FrozB + PBx - Fbarra = mB aB

Bloque B según y ----- > ∑F = NB – PBy = 0

donde

Fbarra = Fuerza que ejerce la barra sobre los bloques A y B

aA = aB = a (ambos bloques están unidos por una barra rígida)

despejando NA y NB  de las ecuaciones según y

NA = PAy = mA g cos 30º 

NB = PBy = mB g cos 30º 

calculando FrozA y FrozB

FrozA = μdA NA = μdA mA g cos 30º

FrozB = μdB NB = μdB mB g cos 30º

sumando las ecuaciones según x,  reemplazando FrozA y FrozB y despejando a

a = 10 m/s² (80 kg (sen 30º - 0,5 cos 30º)  + 8 kg (sen 30º - 0,25 cos 30º)) / ( 80 kg + 8 kg) = 0,87 m/s² < ------ aceleración

reemplazando en la ecuación según x del bloque a, y despejando Fbarra

Fbarra = 80 kg 0,87 m/ s² + 10 m/s² (80 kg (- sen 30º + 0,5 cos 30º) = 15,75 N < ------- fuerza ejercida por la barra

ii) ¿La barra está comprimida o traccionada? ¿Depende el resultado de la ubicación relativa de los bloques?

La barra esta traccionada,  el bloque A es “arrastrado” por el bloque B o bien el bloque A “retiene” al bloque B.

Si el bloque A esta abajo el equilibrio es inestable, y ante cualquier movimiento, la posición de ambos bloques cambia.

b) i) ¿Cuál sería la aceleración y la tensión en la barra si los bloques intercambiaran los coeficientes de rozamiento?

Las ecuaciones no cambian, solo los coeficientes

a = 10 m/s² (80 kg (sen 30º - 0,25 cos 30º)  + 8 kg (sen 30º - 0,5 cos 30º)) / ( 80 kg + 8 kg) = 2,64 m/s² < ------ aceleración

Fbarra = 80 kg 2,64 m/ s² + 10 m/s² (80 kg (- sen 30º + 0,25 cos 30º) = - 15,75 N < ------- fuerza ejercida por la barra

ii) ¿A qué tipo de fuerza estaría sometida la barra en este caso?

Volvemos a calcular las aceleraciones independientes (sin la barra) en este caso

aA = g ( sen 30º - μdA cos 30º ) = 10 m/s² ( sen 30º - 0,25 cos 30º ) = 2,83 m/s²

aB = g ( sen 30º - μdB cos 30º ) = 10 m/s² ( sen 30º - 0,5 cos 30º ) = 0,67 m/s²

El bloque A “arrastra” al bloque B. (por eso da negativa la Fuerza de la barra)

La barra esta traccionada,  el bloque B es “arrastrado” por el bloque A o bien el bloque B “retiene” al bloque A.

c) Si el coeficiente de rozamiento entre cada bloque y el plano es el mismo, calcular la aceleración y la tensión en la barra. ¿Dependen estos resultados de la ubicación relativa de los bloques?

Las ecuaciones no cambian, solo los coeficientes

μdA = μdB = μd =  0,25

a = 10 m/s² (80 kg (sen 30º - 0,25 cos 30º)  + 8 kg (sen 30º - 0,25 cos 30º)) / ( 80 kg + 8 kg) = 2,83 m/s² < ------ aceleración

Fbarra = 80 kg 2,83 m/ s² + 10 m/s² (80 kg (- sen 30º + 0,25 cos 30º) = 0 N < ------- fuerza ejercida por la barra

Volvemos a calcular las aceleraciones independientes (sin la barra) en este caso

aA = g ( sen 30º - μdA cos 30º ) = 10 m/s² ( sen 30º - 0,25 cos 30º ) = 2,83 m/s²

aB = g ( sen 30º - μdB cos 30º ) = 10 m/s² ( sen 30º - 0,25 cos 30º ) = 2,83 m/s²

Las aceleraciones son iguales, la ubicación relativa de los bloques es independiente.

La barra no está traccionada (ni comprimida).  

μdA = μdB = μd =  0,5

a = 10 m/s² (80 kg (sen 30º - 0,5 cos 30º)  + 8 kg (sen 30º - 0,5 cos 30º)) / ( 80 kg + 8 kg) = 0,67 m/s² < ------ aceleración

Fbarra = 80 kg 0,67 m/ s² + 10 m/s² (80 kg (- sen 30º + 0,5 cos 30º) = 0 N < ------- fuerza ejercida por la barra

Volvemos a calcular las aceleraciones independientes (sin la barra) en este caso

aA = g ( sen 30º - μdA cos 30º ) = 10 m/s² ( sen 30º - 0,5 cos 30º ) = 0,67 m/s²

aB = g ( sen 30º - μdB cos 30º ) = 10 m/s² ( sen 30º - 0,5 cos 30º ) = 0,67 m/s²

Las aceleraciones son iguales, la ubicación relativa de los bloques es independiente.

La barra no está traccionada (ni comprimida)

 d) Habiendo analizado todos los casos, ¿de qué depende que la barra esté comprimida o traccionada? Indicar que sucedería en cada caso, si la barra fuera reemplazada por una soga.

La barra está traccionada cuando un bloque arrastra al otro, o bien cuando se mueven juntos. Si se reemplaza por una soga, la soga está estirada.