Dinámica – 42 Fuerza de rozamiento

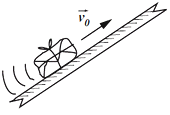
Dinámica 42. Se lanza un paquete hacia arriba, con una velocidad de 3 m/s, por un tablón inclinado con rozamiento no despreciable. El paquete sube en línea recta hasta detenerse, y regresa luego al punto de partida. Asciende durante 2 segundos, y desciende durante 4 segundos.

Calcular:

a) La aceleración que actúa en el ascenso, y la distancia que recorre sobre el plano, hasta detenerse.

Subida

Ecuaciones horarias

x = xo + vo t + ½ a t²

v = vo + a t

donde

x = distancia recorrida

xo = posición de partida = 0

vo = velocidad inicial = 3 m/s

t = tiempo trascurrido = 2 s

a = aceleración

v = velocidad final = 0

reemplazando en la ecuación de la velocidad y despejando a

as = - vo / t =  - 3 m/s / 2s = - 1,5 m/s²  < ------------- aceleración de subida

vo > 0 y as < 0 (desacelerando)

reemplazando en la ecuación de la posición

x = vo t + ½ a t²  = 3 m/s 2s + ½ (- 1,5 m/s² ) ( 2s) ²  = 3 m  < ---------- distancia recorrida

b) Con qué aceleración desciende, y la velocidad con que llega al lugar de partida.

Bajada

Ecuaciones horarias

x = xo + vo t + ½ a t²

v = vo + a t

donde

x = distancia recorrida = 0

xo = posición de partida = 3 m

vo = velocidad inicial = 0

t = tiempo trascurrido = 4 s

a = aceleración

v = velocidad final

reemplazando en la ecuación de la posición y despejando a

ab = (- 2 xo) / t²  = (-2 * 3 m) / (4s)²  = - 0,375 m/s²  < ------------- aceleración de bajada

v = 0 y ab <0 (acelerando)

reemplazando en la ecuación de la velocidad y despejando a

v = ab t =  - 0,375 m/s² 4s  = - 1,5 m/s  < ------------- velocidad final de bajada

c) Sabiendo que la masa del paquete es de 20 kg, determinar la intensidad de la fuerza de rozamiento contra el plano, mientras está en movimiento. Hallar el ángulo de inclinación del plano y el coeficiente de rozamiento dinámico respectivo.

DCL

Ecuaciones de Newton

Cuerpo A subida según x ----- > ∑F = - FrozA –PAx = mA as

Cuerpo A subida según y ----- > ∑F = NA – PAy  = 0

Cuerpo A bajada según x ----- > ∑F = FrozA - PAx = mA ab

Cuerpo A bajada según y ----- > ∑F = NA – PAy  = 0

donde

FrozA = fuerza de rozamiento dinámico entre el cuerpo A y el plano inclinado = μd NA

μd = coeficiente de rozamiento dinámico entre el cuerpo A y  el plano inclinado 

NA = fuerza que ejerce  el plano inclinado  sobre el cuerpo A

PA = Peso del cuerpo A = mA g

PAx = PA sen α

PAy = PA cos α

mA = masa del cuerpo A = 20 kg

as = aceleración de subida = -1,5 m/s²

ab = aceleración de bajada = - 0,375 m/s²

despejando NA de la ecuación según y del cuerpo A (subida y bajada es igual)

NA = PA cos α = mA  g cos α

calculando FrozA

FrozA = μd   mA  g cos α

sumando las ecuaciones según x del cuerpo A de subida y de bajada

– 2 mA g sen α  = mA (as + ab)

despejando sen α

sen α = - (ab + as) / ( 2g) = (- 0,375 m/s²  - 1,5 m/s² ) / ( 2 * 10 m/s² ) = 0,09

α = arco sen (0,09) = 5,38º  < ----------- ángulo del plano inclinado

restando las ecuaciones según x del cuerpo A de subida y de bajada

2 μd   mA  g cos α = mA (ab - as)

despejando μd

μd = (ab - as) / (2g cos α) = (- 0,375 m/s²  + 1,5 m/s²⁾ / (2 * 10 m/s² * cos 5,38º) = 0,056 < ------- coeficiente de rozamiento dinámico

reemplazando en FrozA

FrozA = μd mA g cos α = 0,056 * 20 kg * 10 m/s² * cos 5,38º = 11,25 N  < ------ fuerza de rozamiento