Dinámica 25. Calcular la aceleración de los cuerpos 1 y
2 y la tensión en las sogas en cada caso. Considerar las sogas y poleas como
ideales, y despreciar el rozamiento entre el cuerpo 1 y la superficie
horizontal.
Primero resolver algebraicamente y luego analizar
el movimiento para m1 = 4 kg y m2 = 6 kg.
Caso
A
DCL
Ecuaciones de Newton
Cuerpo 1 según x ----- > ∑F = T = m1 a
Cuerpo 2 según y ----- > ∑F = T - P2 = m2 (-a)
La polea fija ideal cambia la dirección de la Tensión pero no su módulo.
donde
T = Tensión ejercida por la soga
m1, m2 = masas del cuerpo 1 y 2
a = aceleración de los
cuerpos 1 y 2 ( las aceleraciones son iguales, la cuerda es ideal)
P2 = peso del cuerpo 2 = m2 g
Aceleración de los cuerpos 1 y 2
Restando ambas ecuaciones
P2 = m1 a + m2 a
despejando a
a = g m2 / (m1 + m2) < -----------aceleración de los
cuerpos 1 y 2 caso A
Tensión de la soga
Reemplazando a en la primera
ecuación
T = g m1 m2 / (m1 + m2) < ------- tensión de la soga
Caso B
DCL
Ecuaciones de Newton
Cuerpo 1 según x ----- > ∑F = T1 = m1 a1
Polea móvil según y ----- > ∑F = T1 + T1 – T2 = 0 (polea ideal m=0)
Cuerpo 2 según y ----- > ∑F = T2 - P2 = m2 (-a2)
La polea fija ideal solo cambia la
dirección de la Tensión pero no su módulo.
T1, T2 = Tensiones ejercidas por las sogas 1 y 2
m1, m2 = masas del cuerpo 1 y 2
a1, a2 = aceleraciones de
los cuerpos 1 y 2
P2 = peso del cuerpo 2 = m2 g
Aceleración de los cuerpos 1 y 2
Evolución del sistema en el instante t
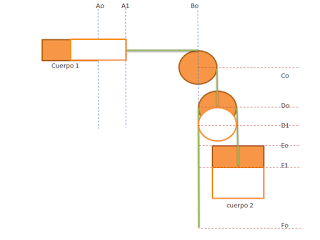
Longitud de la soga = Bo – Ao + π/2 R + Co – Do + π R + Eo – Do = L
π R = la soga rodea la mitad de la polea
π/2 R = la soga rodea un cuarto de la polea
Longitud de la soga = Bo –
A1 + π/2 R + Co – D1 + π R + Eo – D1 = L
Restando la segunda ecuación
de la primera
A1 – Ao – D1 + Do - D1 + Do = 0
Reordenando
(A1 – Ao) - 2 (D1 – Do) = 0
El desplazamiento del punto D
“sigue” al cuerpo 2 (la distancia entre la polea móvil y el cuerpo 2 es fija)
D1 = Do + ½ a2 t2
El desplazamiento del punto
A “sigue” al cuerpo 1
A1 = Ao + ½ a1 t2
Reemplazando ambos
desplazamientos
(½ a1 t2) - 2 (½ a2 t2) =
0
2 a2 = a1
Despejando T1 de la ecuación
cuerpo 1 y T2 de la ecuación del cuerpo 2
T1 = m1 a1
T2 = P2 – m2 a2
Reemplazando ambas en la ecuación de la polea
2 (m1 a1 ) – P2 + m2a2 = 0
Reemplazando a1 y despejando
a2
a2 = g m2 / ( 4 m1 + m2) <
----------- aceleración del cuerpo 2
a1 = 2 a2 = 2 g m2 / ( 4 m1 + m2)
< --------- aceleración del cuerpo 1
Tensión de la soga
Reemplazando a1 en la
primera ecuación y despejando T1
T1 = 2 g m1
m2 / ( 4 m1 + m2) < ------- tensión
de la soga 1
Reemplazando T1 en la
ecuación de la polea y despejando T2
T2 = 2 T1 = 4
g m1 m2 / ( 4 m1 + m2) < ------- tensión de la soga 2
Caso C
DCL
Ecuaciones de Newton
Cuerpo 1 según x ----- > ∑F = T1 = m1 a1
Polea móvil según y ----- > ∑F = T1 – T2 – T2 = 0 (polea ideal m=0)
Cuerpo 2 según y ----- > ∑F = T2 - P2 = m2 (-a2)
La polea fija ideal solo cambia la
dirección de la Tensión pero no su módulo.
donde
T1, T2 = Tensiones ejercidas por las sogas 1 y 2
m1, m2 = masas del cuerpo 1 y 2
a1, a2 = aceleraciones de
los cuerpos 1 y 2
P2 = peso del cuerpo 2 = m2 g
Aceleración de los cuerpos 1 y 2
Evolución del sistema en el instante t
Longitud de la soga 1 = Bo – Ao + π/2 R + Co – Do = L1
Longitud de la soga 2 = Do – Fo + π R + Do - Eo = L2
π R = la soga rodea la mitad de la polea
π/2 R = la soga rodea un cuarto de la polea
Posición del sistema en el instante t (A1, Bo, Co, D1, E1, Fo)
Longitud de la soga 1 = Bo –
A1 + π/2 R + Co – D1 = L1
Longitud de la soga 2 = D1 –
Fo + π R + D1 – E1 = L2
Restando la segunda ecuación
de la primera L1
(A1 – Ao) + (D1 – Do) = 0
Restando la segunda ecuación
de la primera de L2
D1 – Do + D1 – Do – E1 + Eo = 0
2 (D1 – Do) – (E1 - Eo) =
0
Reemplazando D1 – Do
2 (A1 – Ao) = - (E1 – Eo)
El desplazamiento del punto E
“sigue” al cuerpo 2
E1 = Eo - ½ a2 t2
El desplazamiento del punto
A “sigue” al cuerpo 1
A1 = Ao + ½ a1 t2
Reemplazando ambos
desplazamientos
2 (½ a1 t2) = (½ a2 t2)
2 a1 = a2
Despejando T1 de la ecuación
cuerpo 1 y T2 de la ecuación del cuerpo 2,
y reemplazando ambas en la ecuación de la polea
T1 = m1 a1
T2 = P2 - m2 a2
m1 a1 – 2 P2 + 2 m2 a2 = 0
Reemplazando a2 y despejando
a1
m1 a1 – 2 P2 + 2 m2 2 a1 = 0
a1 = 2 g m2 / (m1 + 4 m2) < --------- aceleración
del cuerpo 1
a2 = 4 g m2 / (m1 + 4 m2)
< ----------- aceleración del cuerpo 2
Tensión de la soga
Reemplazando a1 en la
primera ecuación y despejando T1
T1 = 2 g m1
m2 / ( m1 + 4 m2) < ------- tensión
de la soga 1
Reemplazando T1 en la
ecuación de la polea y despejando T2
T2 = T1/2 = g m1 m2 / ( m1 + 4 m2) < ------- tensión de la soga 2
|
m1 = 4 kg
|
m2 = 6 kg
|
|||
|
a1 (m/s2)
|
T1 (N)
|
a2 (m/s2)
|
T2 (N)
|
|
|
Caso A
|
6,00
|
24,00
|
6,00
|
24,00
|
|
Caso B
|
5,45
|
21,82
|
2,73
|
43,64
|
|
Caso C
|
4,29
|
17,14
|
8,57
|
8,57
|







Te comento que tus ejercicios me sirven un monton quiero meter fisica a final. Si sabia que existian tus ejercicios hubiera aprobado el primer parcial.
ResponderEliminarme alegro, suerte en el final.
ResponderEliminarMe cuesta mucho razonar en cómo saber cuál es el cuerpo que tiene más recorrido. Digamos, el que tiene más recorrido es el que posee una aceleración menor en comparación con la del otro cuerpo. Pero, cómo me puedo dar cuenta viendo el dibujo? Por la distribución de las tensiones, de las sogas?
ResponderEliminarEn el caso A el desplazamiento es el mismo.
ResponderEliminarEn los casos B y C el cuerpo 1 se desplaza mas que el cuerpo 2, porque parte del desplazamiento del cuerpo 1 se lo lleva la polea móvil.
Recordar que la soga tiene una longitud fija.
Entonces la aceleración no debería ser mayor siempre en el cuerpo 1, para que en el mismo tiempo recorra el doble de trayectoria que el cuerpo 2 hace con una aceleración de la mitad
EliminarEn el caso A. son iguales.
ResponderEliminarEn el caso B a1 > a2
Pero en el caso C tenes dos sogas (cada una con su longitud fija) por eso a2 > a1
Fijate el análisis de la longitud de la soga en cada caso (ese es el truco de este problema)
Voy a pensar más el análisis, gracias!
Eliminarnoemi sos re crack. <3
ResponderEliminar