Dinámica 25. Calcular la aceleración de los cuerpos 1 y
2 y la tensión en las sogas en cada caso. Considerar las sogas y poleas como
ideales, y despreciar el rozamiento entre el cuerpo 1 y la superficie
horizontal.
Primero resolver algebraicamente y luego analizar
el movimiento para m1 = 4 kg y m2 = 6 kg.
Caso
A
DCL
Ecuaciones de Newton
Cuerpo 1 según x ----- > ∑F = T = m1 a
Cuerpo 2 según y ----- > ∑F = T - P2 = m2 (-a)
La polea fija ideal cambia la dirección de la Tensión pero no su módulo.
donde
T = Tensión ejercida por la soga
m1, m2 = masas del cuerpo 1 y 2
a = aceleración de los
cuerpos 1 y 2 ( las aceleraciones son iguales, la cuerda es ideal)
P2 = peso del cuerpo 2 = m2 g
Aceleración de los cuerpos 1 y 2
Restando ambas ecuaciones
P2 = m1 a + m2 a
despejando a
a = g m2 / (m1 + m2) < -----------aceleración de los
cuerpos 1 y 2 caso A
Tensión de la soga
Reemplazando a en la primera
ecuación
T = g m1 m2 / (m1 + m2) < ------- tensión de la soga
Caso B
DCL
Ecuaciones de Newton
Cuerpo 1 según x ----- > ∑F = T1 = m1 a1
Polea móvil según y ----- > ∑F = T1 + T1 – T2 = 0 (polea ideal m=0)
Cuerpo 2 según y ----- > ∑F = T2 - P2 = m2 (-a2)
La polea fija ideal solo cambia la
dirección de la Tensión pero no su módulo.
T1, T2 = Tensiones ejercidas por las sogas 1 y 2
m1, m2 = masas del cuerpo 1 y 2
a1, a2 = aceleraciones de
los cuerpos 1 y 2
P2 = peso del cuerpo 2 = m2 g
Aceleración de los cuerpos 1 y 2
Evolución del sistema en el instante t
Longitud de la soga = Bo – Ao + π/2 R + Co – Do + π R + Eo – Do = L
π R = la soga rodea la mitad de la polea
π/2 R = la soga rodea un cuarto de la polea
Longitud de la soga = Bo –
A1 + π/2 R + Co – D1 + π R + Eo – D1 = L
Restando la segunda ecuación
de la primera
A1 – Ao – D1 + Do - D1 + Do = 0
Reordenando
(A1 – Ao) - 2 (D1 – Do) = 0
El desplazamiento del punto D
“sigue” al cuerpo 2 (la distancia entre la polea móvil y el cuerpo 2 es fija)
D1 = Do + ½ a2 t2
El desplazamiento del punto
A “sigue” al cuerpo 1
A1 = Ao + ½ a1 t2
Reemplazando ambos
desplazamientos
(½ a1 t2) - 2 (½ a2 t2) =
0
2 a2 = a1
Despejando T1 de la ecuación
cuerpo 1 y T2 de la ecuación del cuerpo 2
T1 = m1 a1
T2 = P2 – m2 a2
Reemplazando ambas en la ecuación de la polea
2 (m1 a1 ) – P2 + m2a2 = 0
Reemplazando a1 y despejando
a2
a2 = g m2 / ( 4 m1 + m2) <
----------- aceleración del cuerpo 2
a1 = 2 a2 = 2 g m2 / ( 4 m1 + m2)
< --------- aceleración del cuerpo 1
Tensión de la soga
Reemplazando a1 en la
primera ecuación y despejando T1
T1 = 2 g m1
m2 / ( 4 m1 + m2) < ------- tensión
de la soga 1
Reemplazando T1 en la
ecuación de la polea y despejando T2
T2 = 2 T1 = 4
g m1 m2 / ( 4 m1 + m2) < ------- tensión de la soga 2
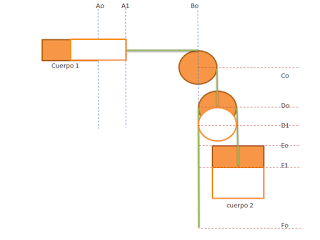
Caso C
DCL
Ecuaciones de Newton
Cuerpo 1 según x ----- > ∑F = T1 = m1 a1
Polea móvil según y ----- > ∑F = T1 – T2 – T2 = 0 (polea ideal m=0)
Cuerpo 2 según y ----- > ∑F = T2 - P2 = m2 (-a2)
La polea fija ideal solo cambia la
dirección de la Tensión pero no su módulo.
donde
T1, T2 = Tensiones ejercidas por las sogas 1 y 2
m1, m2 = masas del cuerpo 1 y 2
a1, a2 = aceleraciones de
los cuerpos 1 y 2
P2 = peso del cuerpo 2 = m2 g
Aceleración de los cuerpos 1 y 2
Evolución del sistema en el instante t
Longitud de la soga 1 = Bo – Ao + π/2 R + Co – Do = L1
Longitud de la soga 2 = Do – Fo + π R + Do - Eo = L2
π R = la soga rodea la mitad de la polea
π/2 R = la soga rodea un cuarto de la polea
Posición del sistema en el instante t (A1, Bo, Co, D1, E1, Fo)
Longitud de la soga 1 = Bo –
A1 + π/2 R + Co – D1 = L1
Longitud de la soga 2 = D1 –
Fo + π R + D1 – E1 = L2
Restando la segunda ecuación
de la primera L1
(A1 – Ao) + (D1 – Do) = 0
Restando la segunda ecuación
de la primera de L2
D1 – Do + D1 – Do – E1 + Eo = 0
2 (D1 – Do) – (E1 - Eo) =
0
Reemplazando D1 – Do
2 (A1 – Ao) = - (E1 – Eo)
El desplazamiento del punto E
“sigue” al cuerpo 2
E1 = Eo - ½ a2 t2
El desplazamiento del punto
A “sigue” al cuerpo 1
A1 = Ao + ½ a1 t2
Reemplazando ambos
desplazamientos
2 (½ a1 t2) = (½ a2 t2)
2 a1 = a2
Despejando T1 de la ecuación
cuerpo 1 y T2 de la ecuación del cuerpo 2,
y reemplazando ambas en la ecuación de la polea
T1 = m1 a1
T2 = P2 - m2 a2
m1 a1 – 2 P2 + 2 m2 a2 = 0
Reemplazando a2 y despejando
a1
m1 a1 – 2 P2 + 2 m2 2 a1 = 0
a1 = 2 g m2 / (m1 + 4 m2) < --------- aceleración
del cuerpo 1
a2 = 4 g m2 / (m1 + 4 m2)
< ----------- aceleración del cuerpo 2
Tensión de la soga
Reemplazando a1 en la
primera ecuación y despejando T1
T1 = 2 g m1
m2 / ( m1 + 4 m2) < ------- tensión
de la soga 1
Reemplazando T1 en la
ecuación de la polea y despejando T2
T2 = T1/2 = g m1 m2 / ( m1 + 4 m2) < ------- tensión de la soga 2
|
m1 = 4 kg
|
m2 = 6 kg
|
|||
|
a1 (m/s2)
|
T1 (N)
|
a2 (m/s2)
|
T2 (N)
|
|
|
Caso A
|
6,00
|
24,00
|
6,00
|
24,00
|
|
Caso B
|
5,45
|
21,82
|
2,73
|
43,64
|
|
Caso C
|
4,29
|
17,14
|
8,57
|
8,57
|