x(t) = t³ – 10 t² – 20 t – 16,
donde
x se expresa en metros y t en segundos.
a)
Calcular la velocidad media de la partícula en el intervalo comprendido entre t = 0 s y t = 12 s.
vm = distancia recorrida / tiempo
empleado = (x(12) – x(0)) / ( 12 – 0)
reemplazando las t en x(t)
x(0) = 0³ – 10 * 0² – 20 * 0 – 16 =
-16
x(12) = 12³ – 10 * 12² – 20 * 12 – 16 =
32
reemplazando la vm
vm = ( 32 – (-16)) / ( 12 – 0 )
= 4 m/s
< ---------- velocidad media
b)
Trazar las gráficas v(t) y a(t).
Para determinar
v(t) = derivada de x(t) = dx(t)/dt
a(t) = derivada de v(t) = dv(t)/dt = derivada segunda de x(t) = d²x(t)/dt²
v(t) = derivada de x(t) = dx(t)/dt
a(t) = derivada de v(t) = dv(t)/dt = derivada segunda de x(t) = d²x(t)/dt²
x(t) = t³ – 10 t² – 20 t – 16 < ------- posición
v(t) = x'(t) = 3 t²
– 20 t - 20 < -------- velocidad
a(t) = x"(t) = 6 t – 20 <
-------- aceleración
Gráfico x vs t
Gráfico v vs t
Gráfico a vs t
Establecer cuales son los intervalos en los que le
movimiento es acelerado y cuales en los que es desacelerado. Determina, si corresponde,
cual/les es/son los instantes en el/los cual/cuales la rapidez es máxima
Analizando
las ecuaciones de v(t) y a(t) (Teorema de Bolzano)
v(t)
es una cuadrática con coeficiente principal es positiva ( 3 > 0) y la ordenada
al origen es negativa (-20>0), se anula en t1 = -0,88 (descartada) y t2 =
7,55.
a(t)
es lineal y tiene un cero en t = 3,33
|
t
|
[0 - 3,33)
|
3,33
|
(3,33 - 7,55 )
|
7,55
|
(7,55 – oo)
|
|
a(t)
|
a(t)<0
|
0
|
a(t)>0
|
a(t)>0
|
|
|
v(t)
|
v(t)<0
|
Mínima
|
v(t)<0
|
0
|
v(t)>0
|
|
(*)
|
acelerado
|
desacelerado
|
acelerado
|
(*)
Signo
de v(t) = signo de a(t) ---- > movimiento acelerado
Signo
de v(t) ≠ signo de a(t) ---- > movimiento desacelerado
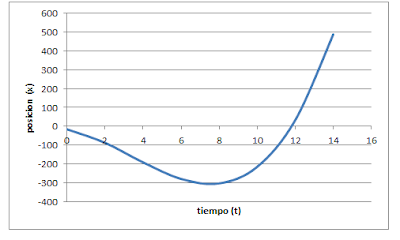


Profe y si quisieramos determinar cuáles son los instantes en los cuales la rapidez es máxima. Que es lo que tendríamos que hacer?
ResponderEliminarla rapidez es máxima en el infinito.
ResponderEliminarVer gráfico v(t)