Energía mecánica 18

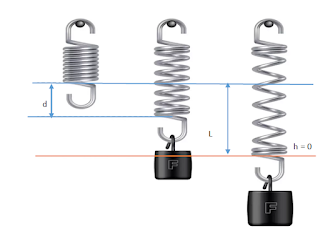
 Un resorte de masa despreciable, inicialmente sin deformación, está colgado del techo. Se fija una pesa al extremo libre y se la deja descender, apoyada en una mano, desplazándose una distancia d hasta alcanzar la posición de equilibrio. Hallar la distancia que descendería la pesa, si después de fijarla al resorte fuera dejada libre desde la misma posición inicial.

Primer movimiento (pesa guiada por una mano)

Fe – P = 0 (en equilibrio)

 

Donde

Fe = fuerza elástica = k d

k = constante del resorte

d = distancia de descenso de la pesa

P = peso = m g

m = masa de la pesa

g = aceleración de la gravedad

 

Reemplazando y despejando k

k = m g / d

 

Segundo movimiento (pesa en caída libre)

ΔEm = Emf - Emi

Donde

ΔEm = variación de la energía mecánica = 0 (no hay fuerzas no conservativas)  

 

Emf = Energía mecánica final = Ecf + Epf + Epef

Ecf = Energía cinética final = 1/ 2 m vf^2 = 0 ( vf = 0 en equilibrio)

Epf = Energía potencial final = m g hf = 0 (hf =0)

Epef = Energía potencial elástica final = 1 /2 k Δx^2

Δx = elongación final del resorte = L

 

Emi = Energía mecánica inicial = Eci + Epi + Epei

Eci = Energía cinética inicial = 1/ 2 m vi^2 = 0 ( vi = 0 se deja caer)

Epi = Energía potencial inicial = m g hi

hi = altura inicial = L

Epei = Energía potencial elástica inicial = 1/ 2 k hi^2 = 0 (hi = 0 resorte sin elongación)

 

 Reemplazando

1 /2 (m g /d) L^2 - m g L = 0

1 /2  L^2 / d - L = 0

Esta ecuación cuadrática tiene dos soluciones

L = 0

L = 2 d