11. Un auto de 1200 kg se desplaza en línea recta durante todo el viaje. Los primeros 10 segundos mantiene una velocidad de 90 km/h. Luego, su conductor aplica los frenos (desacelerando de modo constante) logrando detener el auto en 5 segundos (desprecie el rozamiento con el aire).
a. Realice un diagrama
de cuerpo libre para cada etapa del recorrido incluyendo todas las fuerzas que actúan
sobre el auto y calcule la fuerza de frenado.
DCL 0 < t <
10 seg
Ecuaciones de Newton
Según
x -------- ∑ F = F – Fr = 0 (velocidad constante)
Según
y ---------∑ F = N – P = 0
Donde
F
= fuerza del motor
Fr
= fuerza de rozamiento de las ruedas
N
= reacción del piso
P
= peso del auto
DCL 10 seg < t
< 15 seg
Ecuaciones de Newton
Según
x -------- ∑ F = F – Fr - Ff= m a
Según
y ---------∑ F = N – P = 0
Donde
Ff fuerza de frenado
m
= masa = 1.200 kg
a
= aceleración = (vf – vi)/t
vf
= velocidad final = 0
vi
= velocidad inicial = 90 km/h = 25 m/s
t
= tiempo de frenado = 5 seg
reemplazando
Ff = - m a = - 1.200 kg (0 –
25 m/s) / 5 seg = - 6.000 N
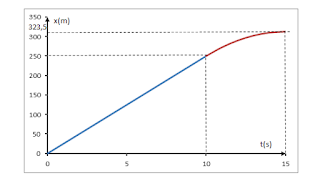
b. Grafique la posición
del auto en función del tiempo para todo el viaje. Incluya en el gráfico los valores
numéricos que crea conveniente para describir cada etapa del viaje.
0 < t < 10
seg - MRU
Ecuación horaria de desplazamiento
x = xo + vo t
donde
x = distancia
recorrida en t
xo = posición
inicial = 0
vo = velocidad
inicial = 25 m/s
t = tiempo
trascurrido = 10 seg
reemplazando en la ecuación horaria
del desplazamiento
x = vo t = 25 m/s 10 seg = 250 m
10 seg < t < 15 seg - MRUV
Ecuación horaria de desplazamiento
x = x1 + vo t + 1/ 2 a t2
donde
x = distancia
recorrida en t
x1 = posición
inicial = posición final del tramo anterior = 250 m
vo = velocidad
inicial = 25 m/s
t = tiempo
trascurrido = (15 seg – 10 seg) = 5 seg
a = aceleración
= (0 – 25 m/s) / 5 seg = - 5 m/s2
reemplazando en la ecuación horaria
del desplazamiento
x = x1 + vo t + 1/ 2 a t2
= 250 m + 25 m/s 5 seg + 1/ 2 (- 5 m/s2) (5seg)2 = 312,5
m


Muy Bueno. Gracias
ResponderEliminar