Física Final Mar 23 T1 – 5 Estática

 Usando una faja (soga) de masa despreciable se ha logrado equilibrar un tronco cilíndrico de

radio R apoyándolo sobre una pared vertical sin rozamiento (ver figura). Si α = 37° y el módulo de la fuerza que ejerce la pared sobre el tronco es de 800 N, determine el peso del tronco.

 

█ 400 N 5 500 N 5 800 N 5 1000 N 5 1300 N 5 1600 N

 

 

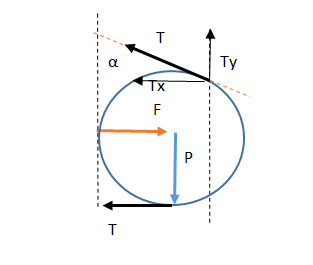
DCL

 

 

∑ Fx = F – Tx - T = 0

∑ Fy = Ty – P = 0

 

Donde

F = reacción de la pared = 800 N

Tx = componente x de la tensión T = T sen 37°

Ty = componente y de la tensión T   = T cos 37°

T = tensión de la soga

P = peso

 

Reemplazando y despejando T de la ecuación según x

T = F / (1 + sen 37°)

 

Reemplazando Y despejando P de la ecuación según y

P = F / (1 + sen 37°) cos 37° = 800 N / (1,6) 0,8 = 400 N