Física 2P Jul22 TC3 – E6 Estática

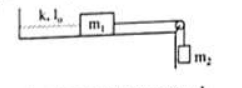
El sistema de la figura, formado por dos masas m1 y m2. Las cuerdas y la polea son ideales. El cuerpo 1 se encuentra unido a la pared mediante un resorte de constante elástica k y longitud natural lo, Se desprecia el rozamiento entre el cuerpo 1 y el piso. Si el sistema se encuentra en equilibrio, la longitud del resorte es igual a:

 

 

□ lo	□ (m1+m2) g/ k + lo	□ m2 g/k
█ m2 g /k +  lo	□ m1 g /k +  lo	□ (m1+m2) g/ k

 

DCL

Cuerpo 1 según x: T – Fe = 0

Cuerpo 2: P2 – T = 0

 

Donde

T = tensión de la cuerda

Fe = fuerza elástica = k (l – lo)

k = constante del resorte

l = longitud del resorte estirado

lo = longitud natural

P2 = peso del cuerpo 2 = m2 g

m2 = masa del cuerpo 2

g = aceleración de la gravedad

 

Sumando ambas ecuaciones

P2 – Fe = 0

 

Reemplazando

m2 g – k (l – lo) = 0

 

Despejando l

l = m2 g / k + lo