Física UBA XXI Final 21 16 Dinámica

Para llevar una caja fuerte a la parte superior de una rampa, una persona tirara de ella empleando una cuerda que en su parte media tiene un resorte de acero cuya constante elástica es 9600 N/m y que en reposo mide 18,0 cm. La rampa forma un ángulo de 15,0º respecto de la horizontal, la caja fuerte tiene una masa de 130 kg y el valor de coeficiente de fricción estático entre la caja y la rampa es 0,345. Cuál es la longitud del resorte cuando la persona tire de la cuerda con la fuerza necesaria para que la caja fuerte empiece a moverse?

□ a. 21,4 cm

□ b. 22,4 cm

□ c. 24,3 cm

■ d. 25,9 cm

 

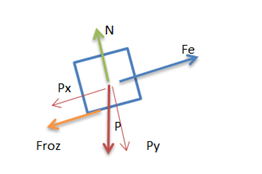
Según x --- > Fe – Px – Froz = 0

Según y --- > N – Py = 0

 

Donde

Fe = fuerza elástica = K Δx

K = constaste elástica del resorte = 9600 N/m

Δx = deformación del resorte = x – xo

x = longitud del resorte estirado

xo = longitud natural = 18 cm

 

Px = componente del peso según x = P sen 15º

P = peso de la caja fuerte = m g

m  = masa de la caja fuerte = 130 kg

g = aceleración de la gravedad  = 9,8 m/s²

Froz = fuerza de rozamiento = µe N

µe = coeficiente de rozamiento estático = 0,345

N = normal (reacción del plano)

Py = componente del peso según y = P cos 15º

 

Reemplazando y despejando Fe

Fe = Px + Froz = Px + µe N = Px + µe Py

Fe = m g sen 15 + µe m g cos 15 = m g (sen 15 + µe cos 15) =

Fe = 130 kg 9,8 m/s² (sen 15 + 0,345 cos 15) = 754,29 N

 

Reemplazando en la Fe y despejando x

x = Fe / K +  xo = 754,29 N / 9600 N/m + 0,18 m = 0,2586 m = 25,9 cm