Física Final Dic 23 TFRB1 7 Cinemática

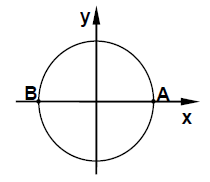
En el instante t = 0 s, un chico en la posición A, comienza a girar sobre una calesita, que parte del reposo en sentido antihorario, describiendo una trayectoria circular de 4 m de radio con aceleración angular constante. En la figura adjunta se esquematiza su trayectoria vista desde arriba. Sabiendo que tarda 16 segundos en completar su primera vuelta, ¿cuál de las siguientes afirmaciones es la única correcta?

 

 

Ecuaciones horarias

α(t) = αo + ωo t + 1 /2 γ t^2

ω(t) = ωo + γ t

 

Donde

α(t) = ángulo barrido en el instante t

αo = ángulo inicial = 0

ωo = velocidad angular inicial = 0 (parte del reposo)

γ = aceleración angular

t = tiempo transcurrido

 

Reemplazando para t = 16 seg

α(16 seg) = 1 /2 γ (16 seg)^2 = 2 π

 

Despejando

γ = 4 π / (16 seg)^2 = π / 64 1/s²

 

 

a = at + ac (ecuación vectorial)

 

Donde

a = aceleración

at = aceleración tangencial = γ R

ac = aceleración centrípeta = ω^2 R

R = radio de la calesita = 4 m

 

Reemplazando

at = γ R = π / 64 1/s²  4 m = π / 16 m/s² tangencial a la trayectoria

ac = (γ t)^2 R = (π / 64 1/s² t)^2 4 m = π^2 / 1024 m/s⁴ t^2 perpendicular a la trayectoria

 

 En t = 0 s, el vector aceleración a del chico apunta hacia el centro de la trayectoria.

Falso

 

Reemplazando t = 0 seg

at = π / 16 m/s²

ac = π^2 / 1024 m/s⁴ t^2 = 0

 

La aceleración es tangencial a la trayectoria

 

 En t = 4 s, el vector aceleración a del chico es perpendicular al vector velocidad v.

Falso

 

Reemplazando t = 4 seg

at = π / 16 m/s²    tangencial a la trayectoria

ac = π^2 / 1024 m/s⁴ (4 seg)^2 = π / 64 m/s²   perpendicular a la trayectoria

 

La aceleración tiene una componente tangencial a la trayectoria

 

 Al pasar por primera vez por B, el vector aceleración del chico es a = (– π²/4 xˆ

 – π/8 ŷ) m/s²

Falso

 

αB = 1 /2 γ t^2 = 1 / 2 π / 64 1/s^{2 t}^2 = π

 

Despejando tB

tB = raíz (128 s²) = 11,31 seg

 

Reemplazando t = 11,31 seg

at = π / 16 m/s²    tangencial a la trayectoria

ac = π^2 / 1024 m/s⁴ (11,31 seg)^2 = π^2 / 8 m/s²   perpendicular a la trayectoria

 

a = π^2 / 8 m/s²  x^ - π / 16 m/s² ŷ

 

 En t = 8 s, el chico pasa por primera vez por B.

Falso

 

Ver anterior

t = 13,31 seg

 

█ En t = 16 s, el vector aceleración del chico es a = (– π²/4 xˆ + π/16 ŷ) m/s²

Verdadero

 

Reemplazando t = 16 seg

at = π / 16 m/s²    tangencial a la trayectoria

ac = π^2 / 1024 m/s⁴ (16 seg)^2 = π^2 / 4 m/s²   perpendicular a la trayectoria

 

a = - π^2 / 4 m/s²   x^ + π / 16 m/s² ŷ

 

 En t = 32 s, el chico completa la segunda vuelta.

Falso

 

Reemplazando t = 32 seg

α = 1 /2 γ t^2 = 1 /2 π / 64 1/s^{2 (}32 seg)^2 = 8 π   Cuatro vueltas