Trabajo y Energía 12

 Una grúa iza verticalmente una caja de caudales de 400 kg, que parte del reposo con aceleración constante durante 2 s, hasta alcanzar una velocidad de 2 m/s; prosigue con ella durante 5 s, para frenar luego y detenerse en otros 2 s.

 

a.     Graficar la velocidad de la caja en función del tiempo.

 

0 < t < 2 seg

v1 = vo + a1 t1

 

Donde

v1 = velocidad final = 2 m/s

vo = velocidad inicial = 0 (parte del reposo)

a1 = aceleración

t1 = tiempo transcurrido = 2 seg

 

Reemplazando y despejando a

a1 = (v1 – vo) / t1  = 2m/s / 2 seg = 1 m/s²

 

v(t) =   1 m/s²  t

 

2 seg < t < 2 seg + 5seg = 7 seg

v(t) = 2 m/s

 

7 seg < t < 7 seg + 2 seg = 9 seg

v2 = v1 + a2 (t3 – t2)

 

Donde

v2 = velocidad final = 0

v1 = velocidad inicial = 2 m/s

a2 = aceleración

t3= tiempo final = 9 seg

t2 = tiempo inicial = 7 seg

 

Reemplazando y despejando a2

a2 = (v2 – v1) / (t3 – t2)  = - 2 m/s / (9 seg – 7 seg)  = - 1 m/s²

 

v(t) =  2 m/s - 1 m/s²  ( t – 7 seg)

 

 

b.     Graficar la fuerza que ejerce el cable, en función del tiempo.

 

0  < t < 2 seg

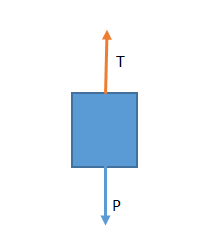
T1 – P = m a1

 

Donde

T1 = tensión

P = peso = m g

m = masa = 400 kg

g = aceleración de la gravedad = 10 m/s²

a1 = aceleración = 1 m/s²

 

Reemplazando y despejando T

T1 = m a + P = m a + m g = 400 kg (1 m/s² +  10 m/s² ) = 4400 N

 

2 seg < t <  7 seg

T2 – P = 0

 

Donde

T2 = tensión

P = peso = m g = 400 kg 10 m/s²  = 4000 N

 

Reemplazando

T2 = P = 4000 N

 

7 seg < t <  9 seg

T3 – P = m a2

 

Donde

T3 = tensión

P = peso = m g = 400 kg 10 m/s²  = 4000 N

a2 = aceleración = - 1 m/s²

 

Reemplazando  y despejando T

T3 = m a2 + P = 400 kg (- 1 m/s² ) + 4000 N  = 3600 N

 

 

c.      Graficar la potencia que desarrolla la fuerza que ejerce el cable, en función del tiempo.

 

 Pot = T v

 

Donde

Pot = Potencia instantánea

T = tensión

v = velocidad

 

0 < t < 2 seg

v(t)  = 1 m/s² t

 

Reemplazando

Pot 1 (t)  = T1 a1 t = 4400 N 1 m/s² t = 4400 W/s t

 

2 seg < t <  7 seg

v(t) = 2 m/s

 

Reemplazando

Pot 2 (t) =  T2 v2 = 4000 N 2 m/s = 8000 W

 

7 seg < t <  9 seg

v(t) = 2 m/s - 1 m/s²  (t – 7 s)

 

Reemplazando

Pot 3(t) = T3 (v2 + a2 t = 3600 J (2 m/s -1 m/s²  (t – 7 s) )  = 7200 W - 3600 W/s (t – 7s)

 

 

d.     A partir de este último gráfico, determinar el trabajo que realiza dicha fuerza, y expresarlo en kWh. Comparar con el trabajo del peso.

W =área de la curva P vs t

 

 

W = area triángulo rojo + rectángulo verde + triangulo amarillo = 8,8 kW 2 seg /2 + 8 kW (7 seg – 2 seg) + 7,2 kW (9 seg – 7 seg) / 2 = 56 kWs (1 h / 3600 s) = 0,0156 kWh

 

 Trabajo de la fuerza peso

 

W = - WT = - 0,0156 kWh

 

e.      Determinar la potencia media desarrollada por el cable.

 

Pot media = W / t = 56 kWs / 9 seg = 6,22 kW

 

f.      Determinar la potencia máxima en todo el proceso.

 

Pot max = máximo grafico Potencia = 8,5 kW

 

g.     ¿Cuál debería ser la potencia mínima del motor de la grúa? (formular las hipótesis necesarias).

 

Potencia minima grua = potencia máxima de la tensión