Estática 2.17. Una
varilla homogénea de 40 cm de
longitud y peso despreciable, se encuentra en equilibrio sostenida en un
extremo (A) por una articulación y en el otro (B) por una soga inextensible y
de masa despreciable.
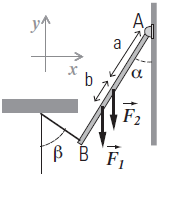
Sobre la varilla actúan las fuerzas
verticales F1 y F2, según muestra la figura.
Siendo α
= 30º; β = 60º; a = 20 cm y b = 4 cm; |F1|
= 5 kgf y |F2| = 10 kgf.
Calcular, expresándolas vectorialmente:
a) La fuerza que ejerce la soga sobre la
varilla.
Apoyo articulado
--- > Reacción Rx y Ry
Diagrama de Fuerzas
Equilibrio ----- > ∑ F = 0 y ∑
M = 0
∑ F = RAy + RAx – F1 – F2 + T = 0 (vectorial)
Según x : RAx – Tx = 0
Según y : RAy - F1 – F2 + Ty = 0
∑ MA = RAx * 0 + RAy * 0 – F1 dF1 – F2 dF2 – T dT = 0
donde
RAx y RAy = fuerza
de reacción del apoyo A
F1 = fuerza 1 = 5
kgf
dF1 = distancia de F1 al punto A,
perpendicular a F1 = (a+b) sen 30º = 0,24 m 0,5 = 0,12 m
F2 = fuerza 2 = 10
kgf
dF2 = distancia de F2 al punto A,
perpendicular a F2 = a sen 30º = 0,20 m 0,5 = 0,10 m
T = tensión de la soga
dT = distancia AB = 0,40 m
Tx = tensión de
la soga según x = T sen 60º
Ty = tensión de
la soga según y = T cos 60º
Reemplazando en las
ecuaciones
Según x --- > RAx – T sen 60º =
0
Según y --- > RAy - 5 kgf
– 10 kgf + T cos 60º = 0
∑ MA = – 5 kgf 0,12 m – 10 kgf 0,10 m + T 0,40 m = 0
Despejando T de la
última ecuación
|T| = (5 kgf 0,12
m + 10 kgf 0,10 m) / 0,40 m = 4 kgf < ---------- módulo de la tensión
Tx = 4 kgf sen 60º = 3,46 kgf
Ty = 4 kgf cos 60º = 2 kgf
T
= (-3,46 kgf ; 2 kgf) < -------- tensión en coordenadas cartesianas
b) La fuerza que hace la articulación en A
sobra la varilla.
Reemplazando Tx
y despejando RAx de la primera ecuación
RAx = 3,46 kgf
<---------- reacción del apoyo según x
Reemplazando Ty
y despejando RAy de la segunda ecuación
RAy = 5
kgf + 10 kgf - 2 kgf = 13 kgf
< --------- reacción del apoyo
según y
RA
= (3,46 kgf ; 13 kgf) < -------- reacción del apoyo A en coordenadas cartesianas

Noemi, buenas, una consulta porque la reacción en x es positiva y la tension negativa?
ResponderEliminarFijate en el sistema de ejes.
ResponderEliminarLos ejes definen x positivo a la derecha e y positivo a la altura
Hola Noemi por qué la RaY va hacia arriba ??
ResponderEliminarFijate en el sistema de ejes.
ResponderEliminarSegún el eje y las dos fuerzas F1 y F2 van hacia abajo, para equilibrarlo se necesita una fuerza hacia arriba (la reacción en la articulación)
Este comentario ha sido eliminado por el autor.
ResponderEliminarHola Noemi, una consulta porque en la sumatoria de momentos pones T y no Ty, porque la Tension (T) no corresponde a ningún eje.
ResponderEliminarEsta es una ecuación vectorial (son todos vectores)
ResponderEliminar∑ F = RAy + RAx – F1 – F2 + T = 0
Cuando se descompone en los ejes x e y
Según x --- > RAx – Tx = 0
Según y --- > RAy - F1 – F2 + Ty = 0
AAA gracias. Tmb me genero duda porque pusiste T y no TY o Tx en
Eliminar∑ MA = RAx * 0 + RAy * 0 – F1 dF1 – F2 dF2 – T dT = 0
∑ MA = RAx * 0 + RAy * 0 – F1 dF1 – F2 dF2 – T dT = 0
ResponderEliminarComo α = 30º y β = 60º; α + β = 30º + 60º = 90º
El momento de la Tensión (T dT) donde dT es la longitud de la barra
Momento = Fuerza * distancia
la distancia se mide perpendicularmente desde el punto de origen de los momentos y la dirección de la fuerza
Hola Noemi , una consulta en esta parte :
ResponderEliminarTx = tensión de la soga según x = T sen 60º porque no T cos 60º si esta en el eje x es horizontal y es cateto adyacente :cos α
Ty = tensión de la soga según y = T cos 60º y esta tiene que ser sen α ... no entiendo me puedes explicar por favor .
El cateto adyacente de beta (60º) es el eje "y"
ResponderEliminarFijate en la grafica