Biofísica 3 opción múltiple 12 Primer Principio

Termodinámica  12 - Un hombre de 70 kg andando en bicicleta entrega una potencia mecánica de 100 W. La tasa metabólica (rapidez con la que varía la energía interna de un ser vivo) para la actividad "andar en bicicleta", para un hombre de 70 kg, es aproximadamente 500 W. Entonces, la cantidad de calor que el hombre entrega al medio exterior si marcha en bicicleta durante 4 horas es, expresada en kilocalorías, aproximadamente:

    a) 600          b) 2.067         c) 2.512     d) 573          █ e) 1.380         f) 100

Potencia = Energía o Trabajo / tiempo

Despejando Trabajo (L) 

L = trabajo (realizado) = 100 W 4 h  (3.600 s/1h) = 1.440.000 J

Primer principio

ΔU = Q - L 

donde

ΔU = variación de la energía interna (perdida) = - 500 W 4 h  (3.600 s/1h) = - 7.200.000 J

Q = calor

Reemplazando

Q = ΔU + L = -7.200.000 J + 1.440.000 J = -5.760.000 J < ---------- calor cedido

Q = 5.760.000 J * 0,24 cal/J = 1.382.400 cal = 1.382 kcal  < ------------- e)

Nota: 1J = 0,24 cal

Biofísica 3 opción múltiple 11 Primer Principio

Termodinámica  11 - Indique cuál de las siguientes afirmaciones es la única verdadera:

a) La energía interna de cualquier sistema termodinámico es sólo función de la temperatura.

Falso

Energía interna es SOLO función de la temperatura para gases ideales.

Para otros sistemas NO es válido.

█ b) La energía interna de un gas ideal es sólo función de la temperatura.

Verdadero

Energía interna es SOLO función de la temperatura para gases ideales.

c) En una evolución isotérmica el sistema no intercambia calor.

Falso

Evolución isotérmica -------- > ΔU (variación de la energía interna) = 0

Primer principio

ΔU = Q - L 

donde

ΔU = variación de la energía interna)Q = calor

L = Trabajo

Reemplazando

ΔU = Q - L = 0 ---------- > Q = L y si L ≠ 0 ------- > Q ≠ 0

d) En un proceso adiabático el sistema no varía la temperatura.

Falso

Evolución adiabática -------- > Q (calor) = 0

Primer principio -------- > ΔU = Q - L ------- > si L ≠ 0 ------- > ΔU ≠ 0 ------- > ΔT ≠ 0

e) Si un sistema no varía su volumen, entonces no realiza ni recibe trabajo.

Falso

El trabajo es SOLO función del volumen  para gases ideales.

Para otros sistemas NO es válido.

f) Si un gas no varía su energía interna entonces no recibe calor.

Falso

ΔU (variación de la energía interna) = 0

Primer principio -------- > ΔU = Q - L ------- > si L ≠ 0 ------- > Q ≠ 0

Biofísica 3 opción múltiple 10 Primer Principio

Termodinámica  10 - Una persona que realiza trabajo mecánico a razón de 34 W, pierde energía interna a razón de 300 W. Si el calor disipado por la persona se distribuye un 70% en radiación y el resto en evaporación del sudor, la cantidad de agua que pierde la persona en una hora es aproximadamente (Lv a 37ºC = 570 cal/g):

a) 2,8 litros    b) 0,5 litros    c) 2,5 litros    d) 0,67 litros    e) 9,3 litros    █ f) 0,12 litros

Potencia = Energía o Trabajo  /  tiempo

despejando trabajo (L)

L = trabajo mecánico (realizado) = 34 W * 3.600 s = 122.400 J

Primer Principio

ΔU = Q - L

donde

ΔU = variación de energía interna (pierde energía) = - 300 W * 3.600 s = -1.080.000 J

Q = calor disipado

 Reemplazado y despejado Q

Q = ΔU + L = - 1.080.000 J  + 122.400 J  = -957.600 J

Qe = calor evaporado = Q * ( 1 – 70%) =  -957.600 J * 0,30 = -287.280 J = -68.662 cal

Nota : 1 cal = 4,184 J

Además

Qe = M * Lv

donde

M = masa de agua evaporada

Lv = calor latente de vaporización  = 570 cal/gr

Reemplazando y despejando M

M = Qe / Lv = -68.662 cal / -570 cal/gr = 120 gr =0,120 kg = 0,120 L < ---------- f)

Biofísica 3 opción múltiple 9 Transmisión de calor

Termodinámica  9 - Si la temperatura de la superficie del Sol fuera la quinta parte de su temperatura actual (ambas expresadas en K), la potencia que la Tierra recibiría del Sol sería, con respecto al actual, aproximadamente:

          a) 16 veces menor           b) la misma                    c) la quinta parte

          d) la mitad                      e) 25 veces menor           █ f) más de 600 veces menor

Ley de Stefan-Boltzmann

Pot = σ ε A T⁴

donde
Pot = potencia
σ = constante de Boltzmann
ε = factor de emisividad
A = superficie emisora
T = temperatura absoluta de la superficie emisora

Temperatura original (o) ----- > Poto = σ ε A To⁴
Temperatura supuesta (s) ----- > Pots = σ ε A Ts⁴

El cociente de ambas ecuaciones
Pots / Poto = σ ε A Ts⁴ / (σ ε A To⁴ ) = Ts⁴ / To⁴  = (Ts / To)⁴

Reemplazando Ts = To/5

Pots / Poto = (Ts / To)⁴= (To/5 / To)⁴ = (1/5)⁴  = 1/625  < ------------- f)

Biofísica 3 opción múltiple 8 Trasmisión de calor

Termodinámica 8. Sean dos recipientes cúbicos A y B conteniendo hielo. Las paredes son adiabáticas, salvo la superior que está expuesta al aire. Los cubos de hielo están a una temperatura inicial de 0ºC y la arista del cubo A es la mitad de la del cubo B. En el mismo lapso en que el cubo A se funde totalmente, la masa de B que se funde es:

a) toda;

b) la cuarta parte de su masa inicial;

█ c) la mitad de su masa inicial;

d) la octava parte de su masa inicial;

e) la décima parte de su masa inicial;

f) la tercera parte de su masa inicial.

Cubo A

Ley de Fourier

Q/Δt = - k A ΔT / x 

donde

Q/Δt = flujo de calor

Q = calor absorbido por el cubo = MA Lf 

MA = masa del cubo = VA δ 

VA = Volumen del cubo A 

δ = densidad del hielo

Lf = calor latente de fusión del hielo

Δt = intervalo de tiempo (igual para los dos cubos)

k = constante de conductividad térmica del hielo

AA = área superior del cubo A

ΔT = variación de la temperatura (igual para ambos cubos, ambos están a 0 ºC y en contacto con la temperatura ambiente)

x = espesor

Reemplazando

VA δ Lf  / Δt  = - k  AA ΔT / x

Despejando Δt

Δt = VA δ Lf x / (- k AA ΔT)

Cubo B

QB/Δt = - k AB ΔT / x 

Donde

QB/Δt = flujo de calor

QB = calor absorbido por el cubo = Mb Lf

Mb = masa derretida del cubo B = Vb δ

Vb = volumen derretido del cubo B

AB = área superior del cubo B

Reemplazando

Vb = (- k AB ΔT / x)  VA δ Lf x / (- k AA ΔT) / δ = AB VA / AA

Con

xA = arista A = 1/2 arista B = 1/2 xB

AA = Area superior A = (xA)^2 = (1/2 xB)^2 = 1/4 (xB)^2 = 1/4 AB

VA = Volumen A = (xA)^3 = (1/2 xB)^3 = 1/8 (xB)^3 = 1/8 Volumen B = 1/8 VB

Reemplazando

Vb = AB (1/ 8) VB / (1/ 4 AB)) = 1/ 2 VB

El volumen derretido es 1 / 2 del volumen total de B

 

 

Biofísica 3 opción múltiple 7 Trasmisión de calor

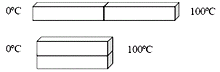
Termodinámica 7.  Una varilla de cobre y otra de acero de igual longitud y sección transversal están soldadas con un extremo en común. El extremo libre de la varilla de cobre se mantiene a 100°C y el extremo libre de la de acero, a 0°C. Las varillas están aisladas lateralmente. El coeficiente de conductividad térmica del cobre es 8 veces el del acero. Una vez que alcanza el régimen estacionario, podemos afirmar que:

a) la temperatura de la unión de ambas varillas es menor que 50°C.

Falso

Ley de Fourier:

Q/Δt = -k A ΔT / Δx

donde

Q/Δt = flujo de calor

k = constante de conductividad térmica (kcu = 8 kac)

A = área de la barra (igual para ambas barras)

ΔT = variación de la temperatura = (T2 – T1)

Δx = longitud de la barra (igual para ambas barras)

Régimen estacionario Q/Δt = constante

Varilla de cobre ---------- > Q/Δt = -kcu A (Tu – 100ºC) / Δx

Varilla de acero ---------- > Q/Δt = -kac A (0ºC – Tu) / Δx

Reemplazando e igualando

- 8 kac A (Tu – 100ºC) / Δx = - kac A (0ºC - Tu) / Δx

8 (Tu – 100ºC) = (0ºC - Tu)

Despejando Tu

Tu = (0ºC + 800ºC) / (8 + 1) = 800ºC /9 = 89 ºC < ----------- temperatura de la unión

Tu = 89ºC  < 50ºC

█ b) la temperatura de la unión de ambas varillas es mayor que 50°C.

Verdadero

Ver ítem a) ------------- >  Tu = 89ºC  > 50ºC

c) las diferencias de temperatura entre los extremos de ambas varillas son iguales.

Falso

Varilla de cobre ---------- > - (89ºC – 100ºC) = 11ºC

Varilla de acero ---------- > - (0ºC – 89ºC) = 89ºC

---------- > ΔTcu = 11ºC ≠ 89ºC = ΔTac

d) la cantidad de calor que, por unidad de tiempo, atraviesa cualquier sección transversal de la varilla de cobre es mayor que la que atraviesa cualquier sección transversal de la varilla de acero.

Falso

Régimen estacionario Q/Δt = constante------ > Qcu/ Δt = Qac/ Δt

e) la cantidad de calor que, por unidad de tiempo, atraviesa cualquier sección transversal de la varilla de cobre es menor que la que atraviesa cualquier sección transversal de la varilla de acero.

Falso

Régimen estacionario Q/Δt = constante ------- > Qcu/ Δt = Qac/ Δt

f) no fluye calor a través de las varillas.

Falso

ΔTcu  ≠ 0ºC  y  ΔTac ≠ 0ºC ---------- >  Q/ Δt ≠  0

Biofísica 3 opción múltiple 6 Trasmisión de calor

Termodinámica  6. Dos barras rectangulares idénticas están unidas como se muestra en la figura superior, de modo que cuando las temperaturas son las indicadas, en régimen estacionario, se transmiten a través de ellas 10 calorías por minuto. ¿Cuál sería la potencia transmitida si estuvieran unidas como se muestra en la figura inferior?

En ambas situaciones el sistema está aislado lateralmente.

a) 20 calorías por minuto

b) 10 calorías por minuto

█ c) 40 calorías por minuto

d) cero

e) 2,5 calorías por minuto

f) 0,25 calorías por minuto

Ley de Fourier:

Q/Δt = -k A ΔT / Δx

donde

Q/Δt = flujo de calor

k = constante de conductividad térmica del hielo

A = área de la barra

ΔT = variación de la temperatura

Δx = longitud de la barra

Configuración superior (a)

(Q/Δt)a = -k Aa ΔT / Δxa

Configuración inferior (b)

(Q/Δt)b = -k Ab ΔT / Δxb

Con Ab = 2Aa y Δxb = Δxa/2

Reemplazando

(Q/Δt)b = -k Ab ΔT/Δxb =  -k 2Aa ΔT/(Δxa/2) = 4 (-k Aa ΔT/Δxa) = 4 * 10 cal/min = 40 cal/min < ---c)

Biofísica 3 opción múltiple 5 Trasmisión de calor

Termodinámica 5. Un iglú tiene forma semiesférica, 2 metros de radio interno, y está construido con bloques de hielo de 40 cm de espesor. Si la temperatura de la cara interior de la pared de la vivienda es de 0ºC y la de la cara exterior, –40 ºC, calcule cuánto calor se transmite por conducción a través de las paredes en una hora (k_hielo = 0,0004 kcal/ºC m s). Observe que la superficie a través de la cual fluye el calor no es constante, como lo es en el caso de una varilla o una pared plana. No obstante, para las condiciones del problema, es una buena aproximación considerarla constante y tomar como radio de la misma el promedio de los radios de las caras interna y externa.

█ a) 4.380 kcal    b) 8.734 kcal    c) 2.189 kcal    d) 1,2 kcal        e) 43,8 kcal      f) 4,18 kcal

Ley de Fourier:

Q/Δt = -k A ΔT / Δx

donde

Q = calor

Δt = tiempo = 1h = 3.600 s

k = constante de conductividad térmica del hielo = 0,0004 kcal/ºC m s

A = área del iglú (media esfera) = ½ 4 π Rprom²

Rprom = radio promedio = (Rext + Rint) / 2 = ( (2m+0,4m) + 2m) / 2 = 2,2 m

ΔT = variación de la temperatura (Tf – Tc) = -40ºC – 0ºC =  -40ºC

Δx = espesor del iglú = 0,4 m

Reemplazando

Q = -0,0004 kcal/ºC m s (2 π (2,2m)² ) (-40ºC) / 0,4 m 3.600 s = 4.380 kcal < -------------- a)

Biofísica 3 opción múltiple 4 Trasmisión de calor

Termodinámica 4. Una varilla metálica, cuyos extremos están uno a 250°C y el otro a 40°C, conduce 75,4 cal/s. Si su longitud y su diámetro se reducen a la mitad, y se colocan sus extremos a las mismas temperaturas que antes, la varilla conducirá (en cal/s):

    a) 75,4     b) 7,5     c) 18,9     d) 754     e) 150,8    █ f) 37,7

Ley de Fourier:

Q/Δt = -k A ΔT / Δx

donde

Q/Δt = flujo de calor

k = constante de conductividad térmica

A = área de la varilla = π (d/2)² = π/4 d²

d = diámetro

ΔT = variación de la temperatura (Tf – Tc) = 40ºC – 250ºC =  -110ºC

Δx = longitud de la varilla

Reemplazando

Q/Δt = -k A ΔT / Δx = -k π/4 d² ΔT / Δx

Varilla original (a)

(Q/Δt)a =-k π/4 da² ΔT / Δxa

Varilla nueva (b)

(Q/Δt)b =-k π/4 db² ΔT / Δxb

Reemplazando  db = da/2 y Δxb = Δxb/2

(Q/Δt)b =-k π/4 (da/2)² ΔT / (Δxa/2) = -k π/4 da² ΔT / Δxb (2/4)

(Q/Δt)b = (Q/Δt)a/2 = 75,4 cal/s / 2 = 37,7 cal/s  < ------------ f)

Biofísica 3 Opción Múltiple 3 Calorimetría

Termodinámica 3. En climas de fuertes heladas, es habitual que los agricultores coloquen dentro de los invernaderos grandes tachos con agua. Un agricultor coloca un barril con 100 kg de agua a 20 ºC en el invernadero donde cultiva verduras. Si la temperatura del agua desciende a 0ºC y luego se congela totalmente, calcule el calor entregado por el agua al interior del invernadero, y cuánto tiempo tendría que haber funcionado un calefactor eléctrico de 1 kW para entregar la misma cantidad de calor que el agua.

       a) 2000 kcal; 2,3 horas        b) 10000 kcal; 11,6 horas      

       c) 8000 kcal; 9,3 horas     █ d) 10000 kcal; 9,3 horas      

       e) 100 kcal; 1,16 horas        f) 100 kcal; 1,16 horas

Q = Q1 + Q2

donde

Q = calor cedido por el agua

Q1 = calor cedido por el agua cuando se “enfría” hasta 0ºC = m ce (Tf - To)

m = masa del agua = 100 kg

ce = calor específico del agua = 1 kcal/kg ºC

Tf = temperatura final = 0ºC

To = temperatura inicial del agua = 20ºC

Q2 = calor cedido por el agua cuando se “congela” = m Ls

Ls = calor latente de solidificación = - 80 kcal/kg

Reemplazando

Q = 100 kg 1 kcal/kgrºC (0ºC – 20ºC) + 100 kg  (- 80 kcal/kg ) = - 10.000 kcal < -------- calor cedido

Calefactor eléctrico

Pot = Q /t

donde

Pot = potencia del calefactor = 1 kW = 1.000 W = 1.000 J/s

Q = calor requerido = 10.000 kcal = 10.000.000 cal = 10.000.000 cal (4,18 J/cal) = 41.800.000 J

t = tiempo requerido

reemplazando y despejando t

t = Q / Pot = 41.800.000 J / 1.000 J/s = 41.800 s = 41.800 s (1 h/3.600 s) = 11,62 h < -- tiempo < - d)

Biofísica 3 Opción Múltiple 2 Calorimetría

Termodinámica 2. Un pedazo de cobre de 150 g que está a una temperatura de 100°C se coloca dentro del vaso de un calorímetro que contiene 200 g de agua a 20°. El vaso es de aluminio y tiene una masa de 37 g. Si la temperatura final de la mezcla es de 25°C. ¿Cuál es el calor específico del cobre (c_cu)? Datos: c_agua= 1 kcal/kg°C c_al= 0,22 kcal /kg°C

█   a) 0,093 kcal/kg°C    b) 0,93 kcal/kg°C      c) 0,052 kcal/kg°C

      d) 0,52 kcal/kg°C      e) 0,064 kcal/kg°C    f) 0,64 kcal/kg°C

Calorímetro = no intercambia calor con el exterior = Σ Q = 0

Σ Q = Qcu + Qcal + Qag

donde

Qcu = calor absorbido/cedido por el cobre = mcu ccu (Tfinal - Tocu)

mcu = masa del cobre = 150 gr

ccu = calor específico del cobre

Tf = temperatura final de la mezcla = 25ºC

Tocu = temperatura inicial del cobre = 100ºC

Qcal = calor absorbido/cedido por el calorímetro = mcal ccal (Tfinal - Tocal)

mcal = masa del calorímetro = 37 gr

ccal = calor específico del calorímetro = calor especifico del aluminio = 0,22 kcal/kg ºC

Tocal = temperatura inicial del calorímetro = temperatura inicial del agua = 20ºC

Qag = calor absorbido/cedido por el agua  = mag cag (Tfinal - Toag)

mag = masa del agua = 200 gr

cag = calor específico del agua = calorímetro = calor especifico del aluminio = 1 kcal/kg ºC

Toag = temperatura inicial del agua = 20ºC

Reemplazando

Σ Q = 150gr ccu (25ºC – 100ºC) + 37gr 0,22cal/grºC (25ºC – 20ºC) + 200gr 1cal/grºC (25ºC – 20ºC) = 0

Despejando ccu

ccu = (- 37gr 0,22cal/grºC (25ºC – 20ºC) - 200gr 1cal/grºC (25ºC – 20ºC)) / (150gr (25ºC – 100ºC))  

ccu = 0,093 cal/gr ºC = 0,093 kcal/kg ºC   < ------------a)