Cinematica 2 MRU 3

2.3 - Juan, cronómetro en mano y ubicado en un tramo rectilíneo de una ruta, estudia el movimiento de los coches que circulan por la misma con velocidad constante. A su derecha, y a 40 metros de él hay un árbol, y más lejos un cartel. En cierto instante ve que un automóvil se le acerca por la izquierda y dispara el cronómetro cuando lo tiene a 100 metros; el auto pasa frente a él 5 segundos después. Utilizando como origen la posición de Juan y los tiempos que indica el cronómetro:

Tabla de valores

Punto A	Punto B	Punto C	Punto D
Auto	Juan	árbol	Cartel
x = -100 m	x  = 0 m	x = 40 m	x = ¿?
t = 0 s	t = 5 s	t = ¿?	t = 10 s
v = cte = ¿?

 a - Hallar el vector velocidad del auto, y la indicación de su velocímetro en km/h. Escribir su ecuación horaria.

La velocidad en función de los datos en el Punto A y el Punto B será:

v  = ( x_B   - x_{A ) /} ( t_B – t_A )

Reemplazando los datos

v  = (0 m   - ( - 100 m)) _/ ( 5s – 0 s ) = 20 m/s

o bien

v  =  20 m/s * ( 1 km / 1000 m) * ( 3600 s/ 1 h) =  72 km/h

la ecuación horaria para el MRU

x = x_o + v ( t – t_o)

reemplazando los valores (en Punto A corresponde a x_{o y} t_o )

x = -100 m + 20 m/s *  t

 b - Hallar en qué instante pasará el auto frente al árbol.

La distancia entre Juan y el árbol es de x_c = 40 m

Despejando t de la ecuación horaria

t_C   = (x_c  - x_{o) /}  v = ( 40 m – ( -100 m)) / 20 m/s  =  7 s

 c - Si cuando el cronómetro indica 10 segundos el auto pasa frente al cartel, cuántos metros hay entre éste y el árbol.

El cronometro marca t_D  = 10 s cuando pasa frente al cartel.

Reemplazando en la ecuación horaria

x_D = -100 m + 20 m/s *  10 s  = 100 m

La distancia d entre el árbol y el cartel

d =  x_D  - x_C     = 100 m – 40 m

d = 60 m

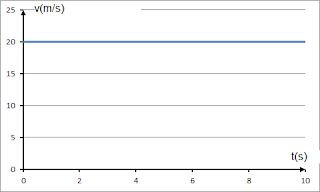
 d - Hacer los gráficos x(t) y v(t), indicando el paso del auto frente al árbol y al cartel.

 Grafico x vs t

Grafico v vs t

 e - Con el mismo origen y sentido positivo, hacer los gráficos para otro auto que se mueve en sentido contrario con la misma rapidez, acotando los tiempos que indicará el cronómetro, hasta que llegue a 100 m a la izquierda de Juan. (Elegir en qué instante se pone en marcha el cronómetro).

Esta pregunta no tiene sentido

Si el auto tiene el mismo origen que el anterior, el auto esta a 100 m a la izquierda de Juan, por lo tanto ya esta a 100 m a la izquierda de Juan